கோள முக்கோணவியல்

முச்செவ்வக முக்கோணம் (Triangle trirectangle)

கோள முக்கோணவியல் (Spherical trigonometry) என்பது கோள வடிவவியலின் ஒரு கிளைப்பிரிவாகும். இது கோள முக்கோணங்களின் பக்கங்கள், கோணங்களுக்கு இடையேயுள்ள அளவீட்டுத்தொடர்புகளை முக்கோணவியல் சார்புகள் மூலமாகத் தருகின்றது. வானியல், புவிமேற்பரப்பியல், வழிச்செலுத்தல் ஆகிய துறைகளில் முக்கியத்துவம் வாய்ந்தது.

கோள முக்கோணவியல், பண்டைக்காலத் துவக்கத்தில் கிரேக்கக் கணதவியலாளர்களால் ஆய்வு செய்யப்பட்டு பின்னர் இசுலாமியக் கணிதவியலாளர்களால் மேம்படுத்தப்பட்டது. துவக்க நவீனகாலத்தின் துவக்கத்தில் கணிதவியலார்கள் ஜான் நேப்பியர், டேலம்பரே ஆகியோரின் பங்களிப்புகளில் மேலும் வளர்ச்சியடைந்து 19 ஆம் நூற்றாண்டில் கணிதவியலாளர் டோதுந்தேர் வெளியிட்ட நூல்மூலம் (Spherical trigonometry for the use of colleges and Schools) முழுமையான வளர்ச்சியடைந்து உருபெற்றது.

முதனிலை விவரங்கள்

மூன்று பெருவட்டங்கள் வெட்டுவதால் உருவான எட்டு கோள முக்கோணங்கள்.

கோளப் பல்கோணிகள்

கோளப் பல்கோணி ('spherical polygon) என்பது ஒரு கோளத்தின் மேற்பரப்பின் மீதுள்ள வளைகோடுகளால் உருவான ஒரு பல்கோணி ஆகும். இவ்வளைகோடுகள், கோளத்தின் மையத்தின் வழியே செல்லும் தளங்களோடு கோளத்தின் மேற்பரப்பு வெட்டிக்கொள்ளும்போது ஏற்படும் வளைகோடுகளாக இருக்கும். கோளப் பல்கோணிகள் எத்தனை பக்கங்கள் கொண்டவையாகவும் இருக்கலாம்.

சமதள வடிவவியலிலுள்ள முக்கோணத்திற்கு ஒத்த கோளப் பல்கோணி இரு தளங்களால் கோளத்தின் மேற்பரப்பில் உருவாகும் பல்கோணியாகும். இப்பல்கோணி "கோளப் பிறை" (spherical lune) அல்லது "இருகோணி" (digon) என அழைக்கப்படுகிறது. கோளப் பிறைக்கு நன்கறியப்பட்ட ஒரு எடுத்துக்காட்டு ஆரஞ்சுப் பழத்தின் ஒரு பகுதியின் வளை மேற்பரப்பாகும். கோள முக்கோணம், மூன்று தளங்களால் கோளத்தின் மேற்பரப்பில் உருவாகிறது. நான்கு தளங்களால் கோளத்தின் மேற்பரப்பில் உருவாகும் பல்கோணிகள் கோள நாற்கரங்கள். இக்கட்டுரையின் இனிவரும் பகுதிகளில் கோள முக்கோணங்கள் சுருக்கமாக முக்கோணங்கள் என்றே குறிப்பிடப்படுகின்றன.

குறியீடு

அலகு கோளத்தின் மீதமையும் அடிப்படை முக்கோணம்.

• முக்கோணத்தின் உச்சிகளும் உச்சிகளில் அமையும் கோணங்களும் A, B, C எனக் குறிப்பிடப்படும்.
• முக்கோணத்தின் கோணங்கள் A, B, C மூன்றும். முக்கோணத்தை உருவாக்கும் தளங்களுக்கு இடைப்பட்ட கோணங்கள். கோணங்களின் அளவு ஆரையன்களில் கொள்ளப்படுகிறது. மேலும்,

π < A + B + C < 3π. (Todhunter, Art.22,32).

• முக்கோணத்தின் பக்கங்கள் a, b, c ஆல் குறிக்கப்படுகின்றன். அலகு கோளத்தின் மீதமையும் முக்கோணத்தின் பக்க நீளங்கள் எண்ணளவில் பெருவட்ட விற்கள் கோளத்தின் மையத்தில் தாங்கும் கோணங்களின் ஆரை அளவுகளுக்குச் சமமாக இருக்கும். மேலும்,

0 < a + b + c < 2π. (Todhunter, Art.22,32).

• கோளத்தின் ஆரத்தின் அளவு ஓரலகாக எடுத்துக்கொள்ளப்படுகிறது. நடைமுறைக் கணக்குகளில் கோளத்தின் ஆரம் R அலகுகள் எனில், பின்னர் தரப்படுள்ள முற்றொருமைகளைப் பயன்படுத்துமுன் முக்கோணங்களின் பக்க நீளங்களை R ஆல் வகுத்துக் கொண்டு கணக்கீடுகள் முடிந்த பின்னர் அவற்றை மீண்டும்  R ஆல் பெருக்கிக்கொள்ள வேண்டும்.

முனைய முக்கோணங்கள்

முனைய முக்கோணம் A'B'C'

முக்கோணம் ABC உடன் தொடர்புடைய கதிர்வரை முக்கோணம் அல்லது முனைய முக்கோணம் பின்னுள்ளவாறு வரையறுக்கப்படுகிறது: விட்டத் தளமானது கோள மேற்பரப்பை வெட்டும்போது BC பக்கத்தை உள்ளடக்கிய பெருவட்டம் உண்டாகிறது. இத்தளத்திற்கு கோளத்தின் நடுப்புள்ளியிலிருந்து ஒரு செங்குத்து வரைந்தால் அது மேற்பரப்பை இரு புள்ளிகளில் சந்திக்கும். அவ்விரண்டில் A புள்ளியோடு இத்தளத்தின் ஒரே பக்கத்திலுள்ள புள்ளி A இன் முனையம் என்று அழைக்கப்பட்டு A′ எனக் குறிக்கப்படும். இதேபோல B′ C′ இரண்டும் வரையறுக்கப்படுகின்றன.

A′B′C′ முக்கோணமானது  ABC முக்கோணத்தின் முனைய முக்கோணம் எனப்படுகிறது. முனைய முக்கோணத்தின் பக்க நீளங்களும் கோணங்களும் கீழுள்ளவாறிருக்கும் (Todhunter, Art.27):

${\begin{alignedat}{3}A'&=\pi -a,&\qquad B'&=\pi -b,&\qquad C'&=\pi -c,\\a'&=\pi -A,&b'&=\pi -B,&c'&=\pi -C.\end{alignedat}}$

முனைய முக்கோணத்தின் முனைய முக்கோணம் எடுத்துக்கொள்ளப்பட்ட மூல முக்கோணமாக இருக்கும்.

கொசைன், சைன் விதிகள்

கொசைன் விதிகள்

கொசைன் விதிதான் கோள முக்கோணவியலின் அடிப்படை முற்றொருமையாகும். சைன் விதி உட்பட்ட பிற கோள முக்கோணவியல் விதிகள் அனைத்து கொசைன் விதியிலிருந்து பெறப்படுகின்றன:

$\cos a=\cos b\cos c+\sin b\sin c\cos A,\!$

$\cos b=\cos c\cos a+\sin c\sin a\cos B,\!$

$\cos c=\cos a\cos b+\sin a\sin b\cos C,\!$

தள முக்கோணவியலின் கொசைன் விதிகளின் உட்கோணங்களின் அளவுகள் சிறியவையாக எல்லைக்குட்படுத்தப்பட்ட சமானங்களாக கோள கொசைன் விதிகள் இருக்கும்.

சைன் விதி

கோள சைன் விதி:

${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.$

கோள முக்கோணத்தின் பக்கங்கள் கோளத்தின் ஆரத்தைவிட மிகச் சிறியதாக இருக்கும்போது இவ்விதியானது கிட்டத்தட்ட தள முக்கோணவியலின் சைன் விதியை ஒத்திருக்கும்.

கோள கொசைன் விதியின் வருவிப்பு

கோள கொசைன் விதி முதலில் டோதுந்தேரால் அடிப்படை வடிவவியல் மற்றும் தள கொசைன் விதிகளைக் கொண்டு நிறுவப்பட்டது. (Todhunter, Art.37). அவர் மேலும் எளிய ஆயமுறை வடிவவியல் மற்றும் தள கொசைன் விதிகளைக் கொண்டும் கோள கொசைன் விதிகளின் வருவிப்பைத் தந்துள்ளார் (Art.60). இக்கட்டுரையில் தரப்படும் வருவிப்பில் திசையன்கள் பயன்படுத்தப்பட்டுள்ளன.

அலகு கோளத்தின் மீதமைந்துள்ள கோள முக்கோணத்தின் உச்சிகளுக்கு கோளத்தின் மையத்திலிருந்து வரையப்பட்ட திசையன்கள் OA, OB, OC. BC வில்லானது கோளமையத்தில் தாங்கும் கோணத்தின் அளவு a:

எனவே OB, OC இரண்டின் புள்ளிப்பெருக்கம்:

OB·OC = cos a.

OA ஐ z-அச்சிலும், xz-தளத்தில் OB ஆனது z-அச்சுடன் உருவாக்கும் கோணம் c எனவும் கொண்டு ஒரு கார்ட்டீசியன் அடுக்களத்தை எடுத்துக்கொள்ள, xy- தளத்தில் OC இன் வீழல் ON ஆகவும், ON, x-அச்சுக்கு இடைப்பட்ட கோணம் A ஆகவும் இருக்கும். எனவே OA, OB, OC திசையன்களின் கூறுகள் பின்னுள்ளவாறு அமையும்:

OA $(0,\,0,\,1)$    OB $(\sin c,\,0,\,\cos c)$    OC $(\sin b\cos A,\,\sin b\sin A,\,\cos b)$.

புள்ளிப் பெருக்கல் OB·OC:

OB·OC${}=\sin c\sin b\cos A+\cos c\cos b$.

OB, OC இரண்டின் இரு புள்ளிப் பெருக்கல்களின் மதிப்புகளையும் சமப்படுத்த:

$\cos a=\cos b\cos c+\sin b\sin c\cos A.$

கோணத்தின் மதிப்பை பக்க அளவுகளின் மூலமாகப் பெறும்வகையில் இதனை மாற்றியமைத்தால் கிடைக்கும் கொசைன் விதியின் மாற்று வடிவம்:

$\cos A={\frac {\cos a-\cos b\cos c}{\sin b\sin c}}.$

வட்ட வரிசைமாற்றத்தைப் பயன்படுத்தி மற்ற இரு கொசைன் விதிகளையும் பெறலாம்.

சைன் விதியின் வருவிப்பு

கீழுள்ள சைன் விதியை வருவிக்கும்முறை டோதுந்தேரின் நூலில் உள்ளது. (Art.40).

$\sin ^{2}A=1-\cos ^{2}A$ முற்றொருமையில் கோள கொசைன் விதியிலிருந்து பெறப்பட்ட $\cos A$ மதிப்பைப் பதிலிட:

${\begin{aligned}\sin ^{2}A&=1-\left({\frac {\cos a-\cos b\cos c}{\sin b\sin c}}\right)^{2}\\[5pt]&={\frac {(1-\cos ^{2}b)(1-\cos ^{2}c)-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}\!b\,\sin ^{2}\!c}}\\[5pt]{\frac {\sin A}{\sin a}}&={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}.\end{aligned}}$

இம்முடிவின் வலப்பக்க மதிப்பில் $a,\;b,\;c$ இன் வட்ட வரிசைமாற்றத்தால் எந்தவொரு மாற்றமும் இருக்காது. எனவே

${\frac {\sin B}{\sin b}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}$.

${\frac {\sin C}{\sin c}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}$.

ஃ${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.$ என நிறுவப்படுகிறது.

மாற்றுமுறை வருவிப்புகள்

மேலே தரப்பட்ட முறையில் மட்டுமல்லாது கோள கொசைன், சைன் விதிகளை மேலும் பல வழிகளில் வருவிக்கலாம். டோதுந்தேர் கொசைன் விதியை இருவழிகளிலும் (Articles 37, 60) சைன் விதியை இருவழிகளிலும் (Articles 40, 42) நிறுவியுள்ளார். புவிமேற்பரப்பியல், கோள வானியல் பாடநூல்களில் வெவ்வேறான நிறுவல்கள் தரப்பட்டுள்ளன. இணையத்தில் மேத்வேர்ல்டில் மேலும் பல நிறுவல்கள் உள்ளன. வீழல் அணிகளின் நேரியல் இயற்கணிதத்தைக் கொண்டு பானர்ஜி அளித்துள்ள நிறுவல்கள் போன்றவையும் உள்ளன.

முற்றொருமைகள்

துணை கொசைன் விதிகள்

முனைய முக்கோணத்திற்கான கொசைன் விதிகள் (Todhunter, Art.47) துணை கொசைன் விதிகள் எனப்படுகின்றன:

மேலே தரப்பட்ட கொசைன்விதிகளில் A = π – a,  a = π – A ... எனப் பதிலிடத் துணை கொசைன்விதிகள் கிடைக்கும்:

${\begin{aligned}\cos A&=-\cos B\,\cos C+\sin B\,\sin C\,\cos a,\\\cos B&=-\cos C\,\cos A+\sin C\,\sin A\,\cos b,\\\cos C&=-\cos A\,\cos B+\sin A\,\sin B\,\cos c.\end{aligned}}$

கோடேன்ஜென்ட் நான்கு-பகுதி வாய்பாடு

முக்கோணத்தின் ஆறு பகுதிகளை (aCbAcB) இன் சுழல் வரிசையாக எழுதலாம். முக்கோணத்தைச் சுற்றித் தொடர்ந்தமையும் நான்கு பகுதிகளை உருவாக்கும் இரு பக்கங்களையும் இரு கோணங்களையும் கோடேன்ஜென்ட் நான்கு-பகுதி வாய்பாடு தொடர்புபடுத்துகிறது (எடுத்துக்காட்டு: (aCbA) அல்லது (BaCb)). இவற்றில் உள், வெளிப் பாகங்கள் உள்ளன. எடுத்துக்காட்டாக (BaCb) இல் உட்கோணம் C, உட்பக்கம் a; வெளிக்கோணம் B, வெளிப்பக்கம் b.

கோடேன்ஜென்ட் நான்கு-பகுதி விதி (டோதுந்தேர், Art.44)

$\cos({\mathsf {inner}}\ {\mathsf {side}})\cos({\mathsf {inner}}\ {\mathsf {angle}})=\cot({\mathsf {outer}}\ {\mathsf {side}})\sin({\mathsf {inner}}\ {\mathsf {side}})-\cot({\mathsf {outer}}\ {\mathsf {angle}})\sin({\mathsf {inner}}\ {\mathsf {angle}}),$

${\begin{array}{lll}{\text{(CT1)}}\quad &\cos b\,\cos C=\cot a\,\sin b-\cot A\,\sin C,\qquad &(aCbA)\\[0ex]{\text{(CT2)}}&\cos b\,\cos A=\cot c\,\sin b-\cot C\,\sin A,&(CbAc)\\[0ex]{\text{(CT3)}}&\cos c\,\cos A=\cot b\,\sin c-\cot B\,\sin A,&(bAcB)\\[0ex]{\text{(CT4)}}&\cos c\,\cos B=\cot a\,\sin c-\cot A\,\sin B,&(AcBa)\\[0ex]{\text{(CT5)}}&\cos a\,\cos B=\cot c\,\sin a-\cot C\,\sin B,&(cBaC)\\[0ex]{\text{(CT6)}}&\cos a\,\cos C=\cot b\,\sin a-\cot B\,\sin C,&(BaCb).\end{array}}$

முதல் வாய்பாட்டின் நிறுவல்:

முதல் கொசைன் விதியை எடுத்துக்கொண்டு அதன் வலப்பக்கத்திலுள்ள $\cos c$ க்கு மூன்றாவது கொசைன் விதியிலிருந்து பதிலிடக் கிடைப்பது:

${\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\&=\cos b\ (\cos a\cos b+\sin a\sin b\cos C)+\sin b\sin C\sin a\cot A\\\cos a\sin ^{2}b&=\cos b\sin a\sin b\cos C+\sin b\sin C\sin a\cot A.\end{aligned}}$

இம்முடிவின் இருபுறமும் $\sin a\sin b$ ஆல் வகுக்க முதல் கோடேன்ஜென்ட் நான்கு-பகுதி வாய்பாடு கிடைக்கும்.

இதேபோல இரண்டாவது, மூன்றாவது கொசைன் விதிகளிலிருந்து CT3, CT5 ஐ நிறுவலாம். 1, 3, 5 வாய்பாடுகளை முனைய முக்கோணத்துக்குப் பயன்படுத்தினால் மீதமுள்ள மூன்று வாய்பாடுகளையும் பெறலாம்.

அரைக்கோண, அரைப்பக்க வாய்பாடுகள்

$2s=(a+b+c),$ $2S=(A+B+C),$ எனில்:

$${\begin{aligned}&\sin {\tfrac {1}{2}}A=\left[{\frac {\sin(s-b)\sin(s-c)}{\sin b\sin c}}\right]^{1/2}&\qquad &\sin {\tfrac {1}{2}}a=\left[{\frac {-\cos S\cos(S-A)}{\sin B\sin C}}\right]^{1/2}\\[2ex]&\cos {\tfrac {1}{2}}A=\left[{\frac {\sin s\sin(s-a)}{\sin b\sin c}}\right]^{1/2}&\qquad &\cos {\tfrac {1}{2}}a=\left[{\frac {\cos(S-B)\cos(S-C)}{\sin B\sin C}}\right]^{1/2}\\[2ex]&\tan {\tfrac {1}{2}}A=\left[{\frac {\sin(s-b)\sin(s-c)}{\sin s\sin(s-a)}}\right]^{1/2}&\qquad &\tan {\tfrac {1}{2}}a=\left[{\frac {-\cos S\cos(S-A)}{\cos(S-B)\cos(S-C)}}\right]^{1/2}\end{aligned}}$$

இவற்றில் வட்ட வரிசைமாற்றத்தின் மூலம் மேலும் 12 வாய்பாடுகளைப் பெறலாம்.

டேலம்பரே ஒப்புமைகள்

1807-1809 இல் டேலம்பரே, காஸ், மொலெவெதெ ஆகிய கணிதவியலாளர்கள் தனித்தனியாக இவ்வாய்பாடுகளை வெளியிட்டனர்.

$${\begin{aligned}{\frac {\sin {\tfrac {1}{2}}(A+B)}{\cos {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}c}}&\qquad \qquad &{\frac {\sin {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}c}}\\[2ex]{\frac {\cos {\tfrac {1}{2}}(A+B)}{\sin {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a+b)}{\cos {\tfrac {1}{2}}c}}&\qquad &{\frac {\cos {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a+b)}{\sin {\tfrac {1}{2}}c}}\end{aligned}}$$

வட்ட வரிசைமாற்றத்தைக் கொண்டும் இதேபோன்ற மேலும் எட்டு வாய்பாடுகளைப் பெறலாம்.

இவற்றை டோதுந்தேர்( Art.54) மற்றும் டேலம்பரே இருவரும் நிறுவியுள்ளனர்.

நேப்பியரின் ஒப்புமைகள்

$${\begin{aligned}&&\\[-2ex]\displaystyle {\tan {\tfrac {1}{2}}(A+B)}={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}(a+b)}}\cot {{\tfrac {1}{2}}C}&\qquad &{\tan {\tfrac {1}{2}}(a+b)}={\frac {\cos {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}(A+B)}}\tan {{\tfrac {1}{2}}c}\\[2ex]{\tan {\tfrac {1}{2}}(A-B)}={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}(a+b)}}\cot {{\tfrac {1}{2}}C}&\qquad &{\tan {\tfrac {1}{2}}(a-b)}={\frac {\sin {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}(A+B)}}\tan {{\tfrac {1}{2}}c}\end{aligned}}$$

வட்ட வரிசைமாற்றத்தைப் பயன்படுத்தி இவற்றைப் போன்ற மேலும் எட்டு வாய்பாடுகளைப் பெறலாம்.

டேலம்பரேவின் வாய்பாடுகளை ஒன்றை மற்றதால் வகுத்து நேப்பியர் வாய்பாடுகளைப் பெறலாம். (டோதுந்தேர், Art.52)

நேப்பியர் வாய்பாடுகளை வகுக்க பாரசீக கணிதவியலாளர் நசீருத்தீன் அத்-தூசீ (1201–1274) கண்டறிந்த கோளத்திற்கான தாஞ்சன்களின் விதி கிடைக்கும்.

$${\frac {\tan {\tfrac {1}{2}}(A-B)}{\tan {\tfrac {1}{2}}(A+B)}}={\frac {\tan {\tfrac {1}{2}}(a-b)}{\tan {\tfrac {1}{2}}(a+b)}}$$

நேப்பியரின் செங்கோண கோளமுக்கோணத்திற்கான வாய்பாடுகள்

கோளமுக்கோணத்தின் மூன்றில் ஏதாவதொரு கோணம் (C என்க) செங்கோணம் (π/2) எனில் மேற்பகுதியிலுள்ள நேப்பியரின் வாய்பாடுகள் மேலும் எளிமையானவையாக மாறும். a, b, c, A, B ஆகியவற்றில் எவையேனும் மூன்றைத் தொடர்புபடுத்தும் பத்து முற்றொருமைகள் கிடைக்கும்.

நேப்பியர் இந்த பத்து முற்றொருமைகளுக்கும் நினைவியைத் தந்துள்ளார். அந்நினைவி "நேப்பியரின் வட்டம்" அல்லது "நேப்பியரின் ஐங்கோணம்" (மேலேயுள்ள வலப்பக்கப் படத்தில் வட்டத்துக்குப் பதில் ஐங்கோணம் எடுத்துக்கொள்ளப்படும்போது) என அழைக்கப்படுகிறது.

முதலில், முக்கோணத்தின் ஆறு கூறுகளை (மூன்று உச்சிக் கோணங்கள், மூன்று பக்கங்களின் விற்கோணங்கள்) அவை முக்கோணத்தின் ஏதாவதொரு சுற்றைப் பொறுத்து அமையும் வரிசையில் எடுத்துக்கொள்ள வேண்டும்:

மேலுள்ள படத்தில் இடப்பக்க முக்கோணத்திற்கு கடிகாரத்திசையில் "a" இலிருந்து தொடங்கினால் aCbAcB கிடைக்கும். அடுத்து கோணம் C க்கு அடுத்தில்லாத கூறுகளை (அதாவது A, c, B) அவற்றின் நிரப்பிகளால் பதிலிட்டு, கோணம் C ஐ நீக்கிவிட வேண்டும். மீதமுள்ளவற்றை ஐங்கோணத்தின் அல்லது வட்டத்தின் ஐந்து வரிசைப்படுத்தப்பட்ட சமமான துண்டுகளாக வரையலாம் (வலப்பக்கப் படம்). இவற்றில் ஒட்டியமையும் மூன்று துண்டுகளில் ஒன்று (நடுவிலுள்ளது) இம்மூன்றில் மற்ற இரண்டுக்கும் அடுத்துள்ளதாகவும் இம்மூன்று தவிர்த்த மீதி இரண்டு துண்டுகளுக்கு எதிராகவும் இருக்கும்.

• நடுப்பகுதியின் சைன் = அடுத்துள்ள இருபகுதிகளின் பெருக்கற்பலனின் டேன்ஜென்ட்
• நடுப்பகுதியின் சைன் = எதிருள்ள இரு பகுதிகளின் பெருக்கற்பலனின் கொசைன்

இதனைப் பயன்படுத்தி $a$ ஐக் கொண்டுள்ள பகுதியிலிருந்து துவங்கக் கிடைக்கும் வாய்பாடுகள்:

$\sin a=\tan(\pi /2-B)\,\tan b=\cos(\pi /2-c)\,\cos(\pi /2-A)=\cot B\,\tan b=\sin c\,\sin A.$

நேப்பியரின் செங்கோண கோளமுக்கோணத்திற்கான பத்து வாய்பாடுகள்: (Todhunter, Art.62) $${\begin{alignedat}{4}&{\text{(R1)}}&\qquad \cos c&=\cos a\,\cos b,&\qquad \qquad &{\text{(R6)}}&\qquad \tan b&=\cos A\,\tan c,\\&{\text{(R2)}}&\sin a&=\sin A\,\sin c,&&{\text{(R7)}}&\tan a&=\cos B\,\tan c,\\&{\text{(R3)}}&\sin b&=\sin B\,\sin c,&&{\text{(R8)}}&\cos A&=\sin B\,\cos a,\\&{\text{(R4)}}&\tan a&=\tan A\,\sin b,&&{\text{(R9)}}&\cos B&=\sin A\,\cos b,\\&{\text{(R5)}}&\tan b&=\tan B\,\sin a,&&{\text{(R10)}}&\cos c&=\cot A\,\cot B.\end{alignedat}}$$

நேப்பியரின் கால்வட்ட முக்கோணத்திற்கான வாய்பாடுகள்

கால்வட்ட கோளமுக்கோணமும் நேப்பியர் நினைவிக்கான நேப்பியரின் வட்டமும்

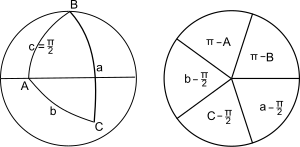
ஒரு கோள முக்கோணத்தின் ஏதாவதொரு பக்கம், கோளமையத்தில் தாங்கும் கோணம் π/2 ரேடியன்களாக இருந்தால் அது கால்வட்ட கோள முக்கோணம் எனப்படும். அலகு கோளத்தில் அத்தகைய பக்கத்தின் நீளம் π/2.

அலகு கோளமையத்தில் செங்கோணத்தைத் தாங்கும் பக்கம் c (அதாவது பக்க நீளம் = π/2) என்க.

இந்த கால்வட்ட முக்கோணத்தின்மற்ற பக்கங்கள், கோணங்களுக்கான நேப்பியர் வாய்பாடுகளை, செங்கோண கோளமுக்கோணத்திற்கான நேப்பியரின் வாய்பாடுகளை முனைய முக்கோணம் A'B'C' க்கு பயன்படுத்திப் பெறலாம் (பக்கங்கள்: a',b',c' ; A' = π − a,  a' = π − A ...): $${\begin{alignedat}{4}&{\text{(Q1)}}&\qquad \cos C&=-\cos A\,\cos B,&\qquad \qquad &{\text{(Q6)}}&\qquad \tan B&=-\cos a\,\tan C,\\&{\text{(Q2)}}&\sin A&=\sin a\,\sin C,&&{\text{(Q7)}}&\tan A&=-\cos b\,\tan C,\\&{\text{(Q3)}}&\sin B&=\sin b\,\sin C,&&{\text{(Q8)}}&\cos a&=\sin b\,\cos A,\\&{\text{(Q4)}}&\tan A&=\tan a\,\sin B,&&{\text{(Q9)}}&\cos b&=\sin a\,\cos B,\\&{\text{(Q5)}}&\tan B&=\tan b\,\sin A,&&{\text{(Q10)}}&\cos C&=-\cot a\,\cot b.\end{alignedat}}$$

ஐந்து-பகுதி விதிகள்

முதல் கொசைன்விதியில் இரண்டாவது கொசைன்விதியைப் பயன்படுத்திப் பதிலிட்டு சுருக்கினால் கிடைக்கும் முடிவு:

$\cos a=(\cos a\,\cos c+\sin a\,\sin c\,\cos B)\cos c+\sin b\,\sin c\,\cos A$

$\cos a\,\sin ^{2}c=\sin a\,\cos c\,\sin c\,\cos B+\sin b\,\sin c\,\cos A$

$\sin c$ காரணியை இருபுறமும் நீக்கக் கிடைப்பது:

$\cos a\sin c=\sin a\,\cos c\,\cos B+\sin b\,\cos A$

இதேபோல மற்ற கொசைன் விதிகள், துணை கொசைவிதிகளில் பதிலிட்டால் அநேக ஐந்து-பகுதி விதிகள் கிடைக்கும். எனினும் அவை அரிதாகவே பயன்படுத்தப்படுகின்றன.

கக்னோலியின் சமன்பாடு

முதல் கொசைன் விதியை $\cos A$ ஆல் வகுத்தால் கிடைப்பது:

$\cos a\cos A=\cos b\,\cos c\,\cos A+\sin b\,\sin c-\sin b\,\sin c\,\sin ^{2}A.$

இதேபோல முதல் துணை கொசைன் விதியை $\cos a$ ஆல் வகுக்கக் கிடைப்பது:

$\cos a\cos A=-\cos B\,\cos C\,\cos a+\sin B\,\sin C-\sin B\,\sin C\,\sin ^{2}a.$

இரண்டையும் கழித்து சைன் விதியிலிருந்து பெறப்படும் $\sin b\,\sin c\,\sin ^{2}A=\sin B\,\sin C\,\sin ^{2}a$ என்ற முடிவையும் பயன்படுத்தினால் கிடைக்கும் சமன்பாடு:

$\sin b\,\sin c+\cos b\,\cos c\,\cos A=\sin B\,\sin C-\cos B\,\cos C\,\cos a$

கோள முக்கோணத்தின் ஆறு-பகுதிகளைத் தொடர்புபடுத்தும் இச்சமன்பாடு கக்னோலியின் சமன்பாடாகும்.

முக்கோணங்களின் தீர்வு

சாய்வு முக்கோணங்கள்

ஒரு கோளமுக்கோணத்தின் ஆறு கூறுகளில் மூன்று, நான்கு அல்லது ஐந்து கூறுகள் தரப்பட்டிருக்கும்போது மீதமுள்ள கூறுகளின் மதிப்பைக் கண்டறிவதே முக்கோணங்களின் தீர்வு காண்பதாகும்.

• ஐந்து கூறுகள் தரப்பட்டால் மீதமுள்ள ஒரு கூறினை எளிதாக சைன் விதியைப் பயன்படுத்திக் கண்டுவிட முடியும்.
• நான்கு கூறுகள் தரப்பட்டிருந்தால் மீதமுள்ள இரண்டைக் கணக்கிடும் வழி கீழே தரப்பட்டுள்ளது.
• மூன்று கூறுகள் மட்டுமே தரப்பட்டிருந்தால் அது ஆறு வகையில் அமையும்:
  • 3 பக்கங்கள்; 2 பக்கங்களும் அவற்றுக்கு இடையேயுள்ள கோணம்
  • எதிருள்ள கோணம்; மூன்று கோணங்கள். (சமதள வடிவவியலில் கடைசி வகைக்கு ஒத்தவகை இல்லை).

ஒரே முறையைப் பயன்படுத்தி எல்லா வகைகளுக்கும் தீர்வு காண முடியாது.

கீழுள்ள படத்தில் ஏழு வகைகளும் காட்டப்பட்டுள்ளன. முக்கோணத்தின் தரப்பட்டுள்ள பக்கங்கள் ஒரு சிறுகுறுக்கோடிட்டும், தரப்பட்டுள்ள கோணங்கள் வில்லிட்டும் காட்டப்பட்டுள்ளன. ஒவ்வொரு படத்தின் கீழும் அந்தந்த வகையில் முக்கோணத்தின் தரப்பட்டுள்ள கூறுகள் குறிக்கப்பட்டுள்ளன.

கீழுள்ள குறியீடுகளில், எடுத்துக்காட்டாக ASA என்பதில், A தரப்பட்ட கோணத்தையும், S தரப்பட்ட பக்கத்தையும், A, S இன் தொடர்முறை முக்கோணத்தில் உள்ள தொடர்முறைக்கு ஒத்ததாக இருக்கும்.

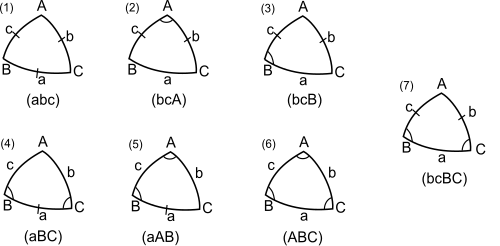
• வகை 1: மூன்று பக்கங்கள் தரப்பட்டுள்ளன (SSS):

கொசைன் விதியைப் பயன்படுத்தி A, B, C ஆகிய மூன்று கோணங்களையும் காணலாம். எனினும் ஈரடியான விடைகளைத் தவிர்க்கும்பொருட்டு அரைக்கோண விதிகள் பயன்படுத்தப்படுகிறது.

• வகை 2: தரப்பட்டவை: இரு பக்கங்களை, இடைப்பட்ட கோணம் (SAS):

கொசைன் விதியைக்கொண்டு மூன்றாவது பக்கத்தைக் கண்டுபிடிக்கலாம். இப்போது இது முதல் வகையாக ஆகிவிடும்.

• வகை 3: தரப்பட்டவை: இரு பக்கங்கள், அவற்றுக்கு எதிருள்ள ஒரு கோணம் (SSA):

சைன் விதியைப் பயன்படுத்தி C கோணத்தைக் கண்டுபிடிக்கலாம். பின்னர் இது வகை 7 ஆகிவிடும். இவ்வகைக்கு ஒன்று அல்லது இரண்டு தீர்வுகள் உண்டு.

• வகை 4: தரப்பட்டவை: இரு கோணங்கள், இடைப்பட்ட பக்கம் (ASA):

(cBaC), (BaCb) இரண்டிற்கும் நான்கு-பகுதி கோடேன்ஜென்ட் வாய்பாடுகளைக் கொண்டு c, b பக்கங்களைக் கண்டுபிடிக்கலாம். பின்னர் சைன்விதியைப் பயன்படுத்தி A கோணத்தைக் கண்டுபிடிக்கலாம்.

• வகை 5: இரு கோணங்கள், எதிர்ப்பக்கம் (AAS):

சைன் விதியைப் பயன்படுத்தி b பக்கத்தைக் காணலாம். பின்னர் இது வகை 7 ஆகிவிடும். இதற்கு ஒன்று அல்லது இரண்டு தீர்வுகள் உண்டு.

• வகை 6: தரப்பட்டவை: மூன்று கோணங்கள் (AAA):

துணை கொசைன் விதியைப் பயன்படுத்தி a, b, c பக்கங்கங்களைக் கண்டுபிடிக்கலாம். ஈரடியான விடைகளைத் தவிர்க்கும்பொருட்டு, அரைப்பக்க வாய்பாடுகள் பயன்படுத்தப்படுகிறது.

• வகை 7: தரப்பட்டவை: இரு கோணங்கள், இரு எதிர்ப்பக்கங்கள் (SSAA):

a, A இரண்டையும் நேப்பியரின் ஒப்புமைகளைப் பயன்படுத்திக் கண்டுபிடிக்கலாம்; அல்லது வகை மூன்றையோ (SSA) அல்லது வகை ஐந்தையோ (AAS) பயன்படுத்தலாம்.

மேலே தரப்பட்டவை தவிர மேலும் பல தீர்வுமுறைகளும் உண்டு. டோதுந்தேர் நூலில் சாய்வு முக்கோணங்களின் தீர்வுகள் குறித்த முழு விவரங்களும் தரப்பட்டுள்ளன.

செங்கோண கோளமுக்கோணங்களைக் கொண்டு தீர்வு காணல்

தீர்வு காணவேண்டிய முக்கோணத்தை இரு செங்கோண முக்கோணங்களாகப் பிரித்தும் தீர்வு காணலாம்.

எடுத்துக்காட்டாக வகை 3 இல் தரப்பட்ட கூறுகள் b, c, B என்க.

• பக்கம் BC பக்கத்திற்கு D புள்ளியில் செங்குத்தாக உள்ள பெருவட்டத்தை உச்சி A இலிருந்து வரைந்துகொள்ள வேண்டும்.
• ABD முக்கோணத்துக்கு நேப்பியரின் விதிகளைப் பயன்படுத்தித் தீர்வு காண வேண்டும்: c, B ஐ பயன்படுத்தி AD, BD பக்கங்களையும் BAD கோணத்தையும் கண்டுபிடிக்க வேண்டும்.
• மீண்டும் ACD முக்கோணத்துக்கும் நேப்பியரின் விதிகளைப் பயன்படுத்தி தீர்வு காண வேண்டும்: AD, b ஐ பயன்படுத்தி DC பக்கத்தையும் C, DAC கோணங்களையும் கண்டுபிடித்துக் கொள்ளவேண்டும்.
• இப்பொழுது இரு முக்கோணங்களிலும் கிடைத்தவற்றைக் கூட்டி A கோணத்தையும் a பக்கத்தையும் பெறலாம்.

பரப்பளவும் கோள மிகுதியும்

ஒரு N-பக்கக் கோள பல்கோணியில் A_n ஆனது பல்கோணியின் n-ஆவது உட்கோணம் எனில் அப்பல்கோணியின் பரப்பளவு (Todhunter, Art.99):

${\text{Area of polygon (on the unit sphere)}}\equiv E_{N}=\left(\sum _{n=1}^{N}A_{n}\right)-(N-2)\pi .$

பல்கோணி முக்கோணமாக இருக்கும்போது அதன் பரப்பளவு:

${\text{Area of triangle (on the unit sphere)}}\equiv E=E_{3}=A+B+C-\pi ,$

இதில் E ஆனது கோள முக்கோணத்தின் கோணங்களின் கூட்டுத்தொகையானது π ரேடியன்களைவிட உள்ள அதிகளவு ஆகும். E ஆனது கோளமுக்கோணத்தின் "கோள மிகுதி" (spherical excess) என அழைக்கப்படுகிறது. மேலேயுள்ள கோள முக்கோணத்தின் பரப்பளவின் வாய்பாடானது அதனைக் கண்டறிந்த பிரெஞ்சு கணிதவியலாளர் ஆல்பர்த்து கிரர்த்தின் பெயரால் "கிரர்த்தின் தேற்றம்" (Girard's theorem) எனப்படுகிறது. இத்தேற்றத்தின் நிறுவல் முன்னர் ஆங்கிலக் கணிதவியலாளர் தாமசு ஃஆரியட்டால் கண்டுபிடிக்கப்பட்டாலும் வெளியிடப்படவில்லை. பல்கோணி அமையும் கோளத்தின் ஆரம் R அலகுகள் எனில் பல்கோணி, முக்கோணம் இரண்டின் மேலுள்ள பரப்பளவு வாய்பாடுகள் R² ஆல் பெருக்கிக்கொள்ளப்படும். முக்கோணத்தின் கோள மிகுதியின் அளவு, கோளத்தின் ஆரவளவைப் பொறுத்ததில்லை

மேலுள்ள முடிவின் மறுதலை முடிவைப் பின்வருமாறு எழுதலாம்:

$A+B+C=\pi +{\frac {4\pi \times {\text{Area of triangle}}}{\text{Area of the sphere}}}.$

கோளமுக்கோணத்தின் பரப்பளவு எதிர்மமாக இருக்காது என்பதால் கோளமிகுதியின் அளவு எப்பொழுதும் நேர்மமாகவே இருக்கும். கோள மிகுதியைக் காண்பதற்குப் பல வாய்பாடுகள் உள்ளன. டோதுந்தேர் பத்து வாய்பாடுகளைத் தனது நூலில் தந்திருக்கிறார். (Art.101—103). அவற்றுள் ஒன்று:

$\tan {\tfrac {1}{4}}E={\sqrt {\tan {\tfrac {1}{2}}s\,\tan {\tfrac {1}{2}}(s-a)\,\tan {\tfrac {1}{2}}(s-b)\,\tan {\tfrac {1}{2}}(s-c)}}$

இதில் $s=(a+b+c)/2$.

கோள மிகுதியைக் காண உகந்த வாய்பாடு

$\tan {\frac {E}{2}}={\frac {\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\sin C}{1+\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\cos C}}.$ ஆகும்.

வெளியிணைப்புகள்

• Weisstein, Eric W., "Spherical Trigonometry", MathWorld. a more thorough list of identities, with some derivation
• Weisstein, Eric W., "Spherical Triangle", MathWorld. a more thorough list of identities, with some derivation
• TriSph A free software to solve the spherical triangles, configurable to different practical applications and configured for gnomonic
• "Revisiting Spherical Trigonometry with Orthogonal Projectors" by Sudipto Banerjee. The paper derives the spherical law of cosines and law of sines using elementary linear algebra and projection matrices.
• "A Visual Proof of Girard's Theorem". Wolfram Demonstrations Project. by Okay Arik
• "The Book of Instruction on Deviant Planes and Simple Planes", a manuscript in Arabic that dates back to 1740 and talks about spherical trigonometry, with diagrams
• Some Algorithms for Polygons on a Sphere Robert G. Chamberlain, William H. Duquette, Jet Propulsion Laboratory. The paper develops and explains many useful formulae, perhaps with a focus on navigation and cartography.
• Online computation of spherical triangles